App - APN
App - Gammu
App - Gammu+
» Gammu+ internals
App - ISTQB Glossary
App - MyGnokii
App - Sobieski
App - True Fenix
Facebook (priv)
Facebook (public)
GitHub
Google Play
HP notebooks forum
LinkedIn
maemo.org
XING
Chrome code (new/Gerrit)
Chrome code (old)
Chrome issues
Firefox Preview c/i
Mozilla Android comp. c/i
Polski
App - APN
App - Bryły
App - Historia polska
App - Poczytaj mi tato
App - Przepisy drogowe
App - Słownik ISTQB
App - Sobieski
App - Straż
Artykuły i pliki
Blog
Artykuły - Chip
Artykuły - Linux+
benchmark.pl
Blog dobreprogramy.pl
Blog spidersweb.pl
TechRacja
Praca dyplomowa
Książka Gdy na was patrzę
Książka Warszawo naprzód
App Store
Blog benchmark.pl
Blog dobreprogramy.pl
Blog spidersweb.pl
Facebook (prywatny)
Facebook (publiczny)
Google Play
LinkedIn
TechRacja na salon24.pl
Categories
Acer (4)
AMD (13)
Android (84)
APN (5)
Apple (28)
App Store (6)
benchmark.pl (19)
chip.pl (7)
CHM (5)
Chrome (5)
dobreprogramy.pl (95)
drogowe (40)
English (130)
English article (23)
English blog (99)
EPUB (7)
Firefox OS (3)
Fizyka (4)
Gammu (62)
Gammu+ (49)
GSM (150)
Hyperbook (10)
ISTQB (3)
jQuery (3)
jQuery Mobile (3)
książka 1 (6)
książka 4 (97)
License (4)
Linux (33)
Linux+ (1)
MyGnokii (6)
Nokia (30)
NTFS (2)
OS (41)
PDF (5)
poczytaj (1)
poem (3)
Polski (233)
polski (235)
Polski artykuł (58)
polski blog (234)
Polski blog (176)
rysunki (2)
S.F. (14)
salon24.pl (177)
Sobieski (8)
Spider's Web (17)
Straż (7)
Tizen (5)
TrueFenix (4)
Ubuntu (5)
Vista (5)
WAT (1)
wiersz (94)
Windows (61)
Windows 7 (11)
x86 (115)
Top 10
N82 review (2008) (200810)
Przepisy drogowe (2012-2021) (151263)
English articles and files (148354)
Polskie artykuły i pliki (144919)
Timeline
2023-03 (5)
2023-02 (1)
2023-01 (13)
2022-12 (9)
2022-11 (10)
2022-10 (12)
2022-09 (14)
2022-08 (4)
2022-07 (3)
2022-06 (4)
2022-05 (3)
2022-04 (9)
2022-03 (11)
2022-02 (9)
2022-01 (5)
2021-12 (6)
2021-11 (13)
2021-10 (11)
2021-09 (11)
2021-08 (4)
2021-07 (5)
2021-06 (12)
2021-05 (3)
2021-04 (4)
2021-03 (4)
2021-02 (5)
2021-01 (4)
2020-12 (4)
2020-11 (5)
2020-10 (1)
2020-09 (9)
2020-08 (5)
2020-07 (2)
2020-06 (1)
2020-05 (6)
2020-04 (3)
2020-03 (2)
2020-02 (2)
2020-01 (8)
2019-12 (2)
2019-11 (11)
2019-10 (1)
2019-09 (3)
2019-06 (1)
2019-05 (1)
2017-12 (2)
2017-11 (2)
2017-10 (2)
2016-01 (1)
2015-09 (2)
2015-08 (1)
2015-06 (1)
2015-05 (1)
2015-04 (1)
2015-03 (2)
2015-01 (1)
2014-10 (1)
2014-09 (2)
2014-07 (2)
2014-06 (5)
2014-05 (7)
2014-04 (3)
2014-03 (9)
2014-02 (5)
2014-01 (8)
2013-12 (7)
2013-11 (4)
2013-10 (10)
2013-09 (5)
2013-08 (9)
2013-07 (5)
2013-06 (1)
2013-05 (2)
2013-04 (3)
2013-02 (3)
2013-01 (7)
2012-12 (5)
2012-11 (5)
2012-10 (7)
2012-09 (2)
2012-08 (2)
2012-07 (2)
2012-06 (1)
2012-05 (2)
2012-04 (4)
2012-03 (6)
2012-02 (2)
2012-01 (3)
2011-12 (1)
2011-11 (1)
2011-04 (2)
2011-02 (2)
2011-01 (3)
2010-12 (5)
2010-11 (1)
2010-10 (2)
2010-08 (1)
2010-07 (2)
2010-06 (3)
2010-05 (9)
2010-04 (11)
2010-03 (14)
2009-12 (4)
2009-11 (2)
2009-10 (2)
2009-05 (1)
2009-03 (1)
2009-02 (1)
2009-01 (1)
2008-07 (1)
2008-05 (1)
2008-04 (1)
2007-12 (3)
2007-11 (2)
2007-10 (2)
2007-09 (3)
2007-08 (1)
2007-07 (2)
2007-06 (4)
2007-05 (4)
2007-04 (2)
2007-03 (5)
2007-02 (3)
2007-01 (6)
2006-12 (5)
2006-11 (5)
2006-10 (4)
2006-09 (2)
2006-08 (1)
2006-07 (6)
2006-06 (3)
2006-05 (2)
2006-04 (5)
2006-02 (1)
2006-01 (2)
2005-12 (1)
2005-09 (1)
2005-07 (1)
2003-11 (1)
2003-09 (5)
2002-11 (2)
2002-10 (14)
2001-07 (1)
2001-05 (2)
2001-01 (1)
2000-10 (1)
2000-07 (1)
2000-06 (1)
2000-03 (1)
1999-06 (2)
1999-04 (2)
Polski
Polski artykuł
Fizyka
Zadania
- 5 stalowych kulek wisi na niciach o jednakowej długości. Po wychyleniu pierwszej odskakuje ostatnia i w końcu wszystkie wahają się razem. Czy:
- pęd kulek jest stały ?
- energia kinetyczna kulek jest stała ?
- w zderzeniu wydziela się ciepło ?
- okres wahań jest stały ?
- napięcie nici jest stałe ?
- 2 kondensatory o pojemnościach C1 i C2 połączono szeregowo, a następnie dołączono do baterii o sile elektromotorycznej E. Oblicz pracę W wyciągnięcia dielektryka spomiędzy okładek pierwszego kondensatora, jeżeli względna przenikalność elektryczna tego dielektryka wynosi e.
- 2 gwiazdy o masie M każda poruszają się po wspólnej orbicie o promieniu R i tworzą w ten sposób gwiazdę podwójną. Oblicz pracę W potrzebną do rozsunięcia gwiazd tak, aby ich orbita była dwa razy większa.
Źródło: K 12-21 - Powietrze o objętości V wypełniające balon ogrzewane jest palnikiem przez otwór w dolnej części powłoki. Gdy temperatura powietrza w balonie osiągnęła wartość T2, balon oderwał się od Ziemi. Oblicz temperaturę początkową T1 powietrza, jeżeli powłoka balonu ma masę M, powietrze - ciśnienie p, mol powietrza - masę m.
- Elektron poruszający się poziomo z prędkością V << C wpada prostopadle do podwójnej, pionowej ściany magnetycznej o grubości 2d. Każda ze ścian ma grubość d i pionowo skierowane pole magnetyczne o indukcji B (jednakowe co do wartości w całej ścianie, ale skierowane do góry w pierwszej, a do dołu w drugiej). Oblicz przesunięcie x toru elektronu po wyjściu z podwójnej ściany (po jej przejściu lub po zawróceniu).
1995/96 (2.03.1996)
- Pytania do pokazanego eksperymentu:
- Uzasadnij, czy pierścień jest wyrzucany przy włączaniu czy przy wyłączaniu prądu.
- Dlaczego w różnych próbach pierścień jest wyrzucany na różne wysokości ?
- Dlaczego wyjęcie monety zmienia przebieg eksperymentu ?
- Kosztem jakiej energii wyrzucany jest pierścień ?
- Dlaczego dołożenie ferromagnetyka zmienia przebieg eksperymentu ?
- 2 sputniki krążą dookoła Ziemi po okręgach o promieniach 2R i 3R i w chwili początkowej oba znajdują się na jednej prostej ze środkiem Ziemi. Po jakim czasie oba sputniki i środek Ziemi znowu znajdą się na jednej prostej, jeżeli R równe jest promieniowi Ziemi ?
- Cząstka a i proton poruszają się po tej samej prostej i w tym samym kierunku. W chwili, gdy odległość między cząstkami jest równa r, cząstka a porusza się z prędkością V, a proton z prędkością U. Oblicz, w jakiej odległości x znajdą się te cząstki w chwili, gdy cząstka a zatrzyma się, jeżeli nie zaszła reakcja jądrowa między cząstkami.
- Naczynie o objętości V zawiera hel pod ciśnieniem p i temperaturze T oraz masę M promieniotwórczego polonu ulegającego rozpadowi a. Oblicz ciśnienie p1 w naczyniu po całkowitym rozpadzie polonu, jeżeli masa atomu polonu wynosi m, a masa atomu Pb powstającego po rozpadzie m1 i ciepło właściwe helu przy stałej objętości wynosi Cv, a ołowiu Cb. Załóż ponadto pomijalnie małą pojemność cieplną ścianek naczynia i ich adiabatyczność oraz tak dużą odległość preparatu promieniotwórczego od ścianek naczynia, że żadna cząstka a nie może opuścić naczynia. Masy molowe helu - mHe i polonu - mPo.
- Jedna z płytek płaskiego i początkowo nienaładowanego kondensatora próżniowego o pojemności C i powierzchni płytek S oświetlona jest całkowicie światłem o długości fali l i o natężeniu światła I. Praca wyjścia z oświetlonej płytki wynosi W. Po jakim czasie t i do jakiego potencjału U naładuje się ten kondensator, jeżeli każdy foton wybija elektron z oświetlonej płytki, a wybity elektron nie opuszcza kondensatora ?
1996/97 (8.03.1997)
- Zadanie doświadczalne. Należy wyjaśnić:
- Dlaczego wskaźnik elektroskopu zmniejsza wychylenie, gdy układ jest oświetlany lampą łukową z elektrodami węglowymi (Eksperyment 1).
- Dlaczego szybkość zmian wychylenia wskaźnika maleje, gdy lampę odsunie się od układu (Eksperyment 2).
- Dlaczego położenie wskaźnika nie zmienia się, gdy między układem i lampą znajduje się szklana płyta (Eksperyment 3).
- Dlaczego położenie wskaźnika nie zmienia się pomimo oświetlenia (Eksperyment 4).
- Jak można zmodyfikować Eksperyment 4, aby wskaźnik elektroskopu zmniejszał wychylenie ?
- Przestrzeń kosmiczną otaczającą planetę o masie M0 i promieniu R wypełnia jednorodnie tzw. ciemna materia, która oddziaływuje grawitacyjnie, ale praktycznie nie stawia oporu ruchu poruszającym się obiektom. Wokół planety krąży satelita po orbicie kołowej o promieniu 3R z I prędkością kosmiczną charakterystyczną dla tej planety. Oblicz gęstość czarnej materii.
- Między 2 metalowe płyty o wymiarach a*b każda włożono nieprzewodzący prostopadłościan gumowy o wymiarach a*b*d. Jedną z płyt naładowano ładunkiem Q, natomiast drugą ładunkiem -Q. Oblicz energię układu wiedząc, że stała dielektryczna gumy jest równa e, a jej moduł Younga Y. Zaniedbaj wpływ mas płyt.
- Cylinder zamknięty jest ruchomym tłokiem o powierzchni S, który umocowany jest do dna cylindra sprężyną o stałej k. Wewnątrz układu znajduje się n0 moli gazu o temperaturze T. W pewnym momencie w cylindrze otwarto zaworek pozwalając wylatywać do atmosfery u molom gazu w jednostce czasu (n0 >> u*1 s), zachowując temperaturę oraz równowagę termodynamiczną. Wyznacz położenie tłoka w funkcji czasu pamiętając, iż ciśnienie atmosferyczne jest równe pA. Przyjmij, że sprężyna jest tak krótka, iż jej wydłużenie jest równe odległości tłoka od dna cylindra. Zaniedbaj masę tłoka.
- Elektrony poruszają się w cyklotronie w polu magnetycznym o indukcji B po orbicie o promieniu R. W pewnej chwili między duantami przyłożono zsynchronizowane, oscylujące napięcie V. Po wykonaniu N obiegów (od momentu włączenia napięcia) przyśpieszoną wiązkę elektronów skierowano na target wytwarzając promieniowanie X. Oblicz minimalną długość fali tego promieniowania.
- W szczelnie zamkniętym, szklanym pojemniku znajdowała się na dnie niewielka ilość wody. Układ woda-powietrze był w stanie równowagi termodynamicznej. Następnie po doprowadzeniu suchego powietrza z kompresora ciśnienie w pojemniku wzrosło. Po zamknięciu zaworu odłączono przewód doprowadzający sprężone powietrze i odczekano kilka minut, by układ woda-powietrze w pojemniku znalazł się ponownie w stanie równowagi.
- Wyjaśnij, czy po doprowadzeniu do pojemnika suchego powietrza, w trakcie ustalania się równowagi termodynamicznej, objętość wody na dnie była stała, czy ulegała zmianie ?
Następnie otwarto zawór.- Czy po otwarciu zaworu, w trakcie rozprężania, temperatura powietrza pozostałego w pojemniku ulegała zmianie ? Odpowiedź uzasadnij korzystając z praw termodynamiki.
- Wyjaśnij, dlaczego promień światła przecinający szklany pojemnik staje się wyraźnie widoczny po otwarciu zaworu ?
- Do sprężyny o stałej sprężystości k przymocowano klocek o masie m. Drugi koniec sprężyny przytwierdzono do ściany. Następnie klocek odciągnięto od położenia równowagi na odległość A0 i puszczono swobodnie. Ile razy w ciągu całego ruchu klocek będzie przechodził przez położenie równowagi (sprężyna nienaprężona) ? Dane są współczynniki tarcia kinetycznego m i statycznego ms= b*m (1 < b < 2) klocka o podłoże. Masę sprężyny powinieneś zaniedbać.
- Wilgotne powietrze unosi się adiabatycznie do góry. Przy powierzchni Ziemi ciśnienie wynosi p0 = 100 kPa, temperatura t0 = 20°C. Gdy powietrze unosi się ku górze, przy ciśnieniu 80 kPa zaczynają tworzyć się chmury. Na jakiej wysokości nad Ziemią znajduje się podstawa chmur (powinieneś przyjąć, że gęstość powietrza maleje liniowo z wysokością) ? Wykładnik adiabaty dla powietrza k = 1,4; masa molowa powietrza m = 29 g/mol.
- Rysunek przedstawia schemat obwodu elektrycznego. Zmiana wartości oporu R2 w tym układzie nie wywołuje zmiany wskazań amperomierza. Jaki warunek muszą spełniać parametry elementów obwodu, aby było to możliwe?

- 2 identyczne głośniki oddalone od siebie o 10 m podłączone są do jednego generatora dającego sygnał o częstości u = 21,5 Hz. Prędkość dźwięku w powietrzu wynosi 343 m/s.
- Wytłumacz, dlaczego odbiornik znajdujący się w punkcie A (patrz rysunek) zarejestruje minimum natężenia dźwięku docierającego z obu głośników.
- Po jakim torze należy przemieszczać odbiornik w płaszczyźnie xy tak, aby nadal rejestrował on minimum natężenia dźwięku (znajdź zależność pomiędzy współrzędnymi x i y odbiornika, dla których rejestruje minimum natężenia dźwięku) ?

- W obwodzie przedstawionym na rysunku do źródła prądu zmiennego podłączono szeregowo kondensator i cewkę o regulowanej indukcyjności (początkowo nie ma żarówki). Znajdują się w nim również trzy woltomierze prądu zmiennego.
- Dlaczego suma napięć skutecznych na kondensatorze VC i cewce VL w tym obwodzie nie jest równa napięciu skutecznemu na źródle prądu e ?
- Następnie do obwodu włączono żarówkę (tak, jak na rysunku). Dlaczego tylko dla pewnej określonej wartości indukcyjności (gdy VC = VL) żarówka świeci jasno, a dla innych wartości nie świeci (lub ewentualnie świeci mniej intensywnie) ?
Przyjmij, że zakłócenia spowodowane przewodami doprowadzającymi, jak i niedoskonałością woltomierzy, są pomijalne.
- Ciężarek zawieszony na nici nie będzie wskazywał dokładnie kierunku przyciągania ziemskiego, lecz odchyla się nieco od tego kierunku. Dla jakich szerokości geograficznych, tj. dla jakich wartości kąta a to odchylenie (różnica b - a) ma wartość maksymalną, a dla jakich minimalną ? Przyjmij, że Ziemia jest jednorodną kulą. Pomocne mogą być następujące wzory i przybliżenia:
tg(x) - tg(y) = sin(x - y)/(cos(x) cos(y));
sin(2x) = 2 sin(x) cos(x)
dla |x| << 1 sin(x) @ x i 1/(1 - x) @ 1 + xUwaga: Na rysunku odchylenie i rozmiary ciężarka zawieszonego na nici zostały (w celu wprowadzenia przejrzystych oznaczeń) znacznie powiększone.

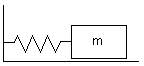
- W układzie przedstawionym na rysunku masy m1 i m2 znajdują się w chwili początkowej w spoczynku, a sprężyna o stałej sprężystości k jest nienaprężona. Jaką wartość powinien mieć współczynnik tarcia mmiędzy masą m1 i podłożem, aby masa m2 po osiągnięciu najniższego położenia nie rozpoczęła ruchu powrotnego do góry ? Przyjmij, że współczynnik tarcia kinetycznego nie różni się do współczynnika tarcia statycznego. Pomiń masę sprężyny i tarcie pomiędzy nicią i bloczkiem.

- W temperaturze T i przy ciśnieniu p gęstości powietrza, czystego tlenu i czystego azotu wynoszą odpowiednio:
 ,
,  ,
,  . Zakładając, że obecne są tylko te dwa gazy, oblicz procentową zawartość azotu w powietrzu.
. Zakładając, że obecne są tylko te dwa gazy, oblicz procentową zawartość azotu w powietrzu. - Dwa ogniwa i trzy kondensatory połączono tak jak na rysunku. Znajdź napięcie na każdym z kondensatorów.

Rozwiązania i odpowiedzi
- W = 2R5(2p/T)4/G
- wskazówki:
- Ilość wody nie ulega zmianie (ciśnienie pary nasyconej nie zależy od ciśnienia pozostałych składników powietrza).
DU = Q - W I zasada termodynamiki Q = 0 Przemiana adiabatyczna (krótki czas) W > 0 Wykonywana jest praca nad powietrzem atmosferycznym DU < 0 Temperatura maleje -
Zachodzą dwa procesy:
- Dt < 0
Patrz punkt b - Dp < 0
Dla pary nasyconej
Proces 1 przeważa nad procesem 2, stąd para wodna osiąga stan przesycenia i następuje skraplanie. Wiązka światła jest rozpraszana na kroplach wody.
- Ilość wody nie ulega zmianie (ciśnienie pary nasyconej nie zależy od ciśnienia pozostałych składników powietrza).
-
kA2n-1/2 - kA2n/2 = mgm(An-1 + An)
A2n-1 - A2n= a(An-1 + An)
a = 2mgm/kKolejne maksymalne wychylenia klocka z położenia równowagi różnią się o stałą wartość:
An-1 - An = aAby klocek rozpoczynający ruch z odległości An-1 od położenia równowagi znalazł się po drugiej stronie położenia równowagi potrzeba, by An > 0. Z tego wynika, że An-1 > a.
Jeśli bowiem An-1 < a, to możliwe są dwa przypadki:
- klocek nie pokona tarcia statycznego
- może rozpocząć ruch, ale zatrzyma się przed osiągnięciem położenia równowagi
An > 0 => An-1 > aOstatni warunek obejmuje:
- przejście przez położenie równowagi
- pokonanie tarcia statycznego (b< 2)
A0 - (n - 1)a > a
n = [A0/a] -
wzory:
- pV = mRT/m
- r = pm/RT
- pVk= p0V0k
- p0 - p =
 gh
gh
 = (r0+r)/2
= (r0+r)/2
Z 1 i 3 wynika, że (p/p0)(1 - k) / k =T0/T
Z 2 i 5 wynika, że =m(p0 + p (p/p0)(1 - k) / k)/2RT0 = 1,1 kg/m3
=m(p0 + p (p/p0)(1 - k) / k)/2RT0 = 1,1 kg/m3
h = (p0-p)/g = 1900 m
= 1900 m
-
Można np. zastosować prawa Kirchoffa dla obu oczek:
- e2 - i2R2 - (i1+i2)R - i2r2 = 0
- e1 - (i1+i2)R - i1r1 = 0
Rozwiązując ten układ równań otrzymujemy:i2 = (e2(R+r1) - e1R)/(R2R + Rr2 + R2r1 + Rr1 + r2r1)
Aby przez opornik R2 nie płynął prąd, i2 = 0
Podstawiając do wzoru na i2 i przekształcając dostajemy, że e2 = e1R/(R+r1)
Należy też pamiętać, że r2 >> R i r2 >> r1
-
- l = V/f = 16 m
Dr = l/2 = 8 m
Różnica dróg do punktu A z obu głośników wynosi 8 m. Jest to akurat połowa długości fali dźwiękowej i warunek na minimum interferencyjne. - r1 - r2 = l/2
 -
- = 8
= 8
9x2 - 16y2 = 144
- l = V/f = 16 m
-
- ˝VL - VC˝= e
- Gdy VL = VC zawada ma wartość minimalną, a prąd osiąga maksimum.
-

mg / sin (180° - b) = mw2Rzcos a/ sin (b - a)
b - a @ (w2RZ cos a sin b)/g @ (w2RZsin 2a) / (2g)
max (b - a) Ţa = 45°
min (b - a) Ţa = 0° Ú a = 90° -
0,5kx2 + mm1gx = m2gx
kx Ł m2g + mm1g
Ţ m ł m2/(3m1) -
 +
+ =
=  Ţ
Ţ 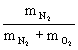 =
=
- Z układu trzech równań:
- e1 = V3 + V2
- e2 = V2 - V3
- V1C1 = V2C2 + V3C3
wynika, że:V1 = [(e1 + e2)C2 + e1C3]/(C1 + C2 + C3)
V2 = [(e1 + e2)C1 + e2C3]/(C1 + C2 + C3)
V3 = (e1C1 - e2C2)/(C1 + C2 + C3)